微積分のセミナーをすることになった

微積分をきちんと勉強しなおす.

かねてより幾度も言っているが, 微積分をきちんと勉強しなおすことにした. 私の目的は微積分の基本的な考え方, 手法, 定理や命題の依存関係, その応用をきちんと捉え直すことにある.
また解析的な視点のみならず, 幾何的な視点を強調して勉強したいと思って勉強し直そうと想っている. テキストは, 斎藤毅先生の, 『微積分』 (東京大学出版会, 2013) の予定だ.

この本を採用した理由

この本を採用した理由は次である.

微分方程式について載っている.

意外と, 古典的な解析の教科書にはこの点は強調して書かれていないことも多いのではないだろうか.

物理学との関連も書かれている.
そんなに厚くない.

最後まで読めばおそらく知らないこと, あるいは抽象的にしか勉強する機会もないことを具体的な実感を伴って勉強できるのではないかと思う.

抽象と具体は表裏一体だ. 抽象的な数学が出来る人は具体例に強い.

第 3 章から読もうと思っている.

縦線集合について

しかし早速面白いことを発見した. いや, 僕が知らなかっただけなのだけれど.
${\varepsilon-\delta}$ 論法を陽に使う議論って, 当たり前だがそれが必要だからそう議論する. 言い換えれば, ${\varepsilon-\delta}$ 論法って古典的な微分積分学の範囲を越えるとあまり陽には出てこないが, それは古典解析の範囲で基礎的な証明をシッカリハッキリクッキリ理解してるから使えるんだよね. 何が言いたいのかというと, 次の命題である.

縦線集合

${(a, b)}$ で定義された 連続関数 ${k(x), l(x)}$ に対し, 集合 ${U}$ を,

${ \begin{align} U = \{(x, y)\in \mathbb{R}^2 \mid a < x < b , k(x) < y < l(x)\} \end{align} }$
と定める. このとき, ${U}$ を縦線集合という.

命題

縦線集合は開集合である.

まぁお絵かきをしよう. 手書き*1を携帯で撮ったのでななめになってるけどそこはたぶん本質じゃないので気にしないで……

f:id:hikaru515:20151004201525j:plain

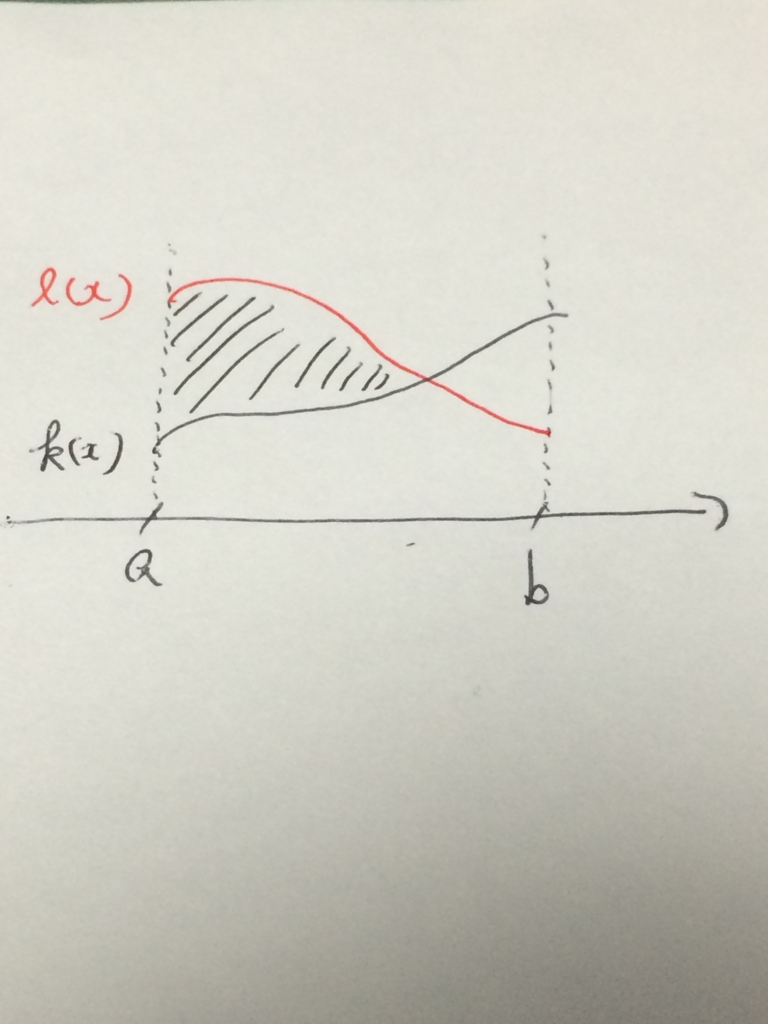
まぁとりあえず縦線集合のあの定義を見たらこういう図形を思い描いて, 「なるほど開集合っぽいな」という印象を受けると思う.
書いてあるけど, 赤線が ${l(x)}$ のグラフで, 黒線が ${k(x)}$ のグラフである.

ところで, 地味に強調してあるが ${k(x), l(x)}$ が連続関数という仮定が必要である. それはなぜ必要なんだろう……と考えてみると, ちょっと頑張ると次のような図が書ける.

f:id:hikaru515:20151004202659j:plain

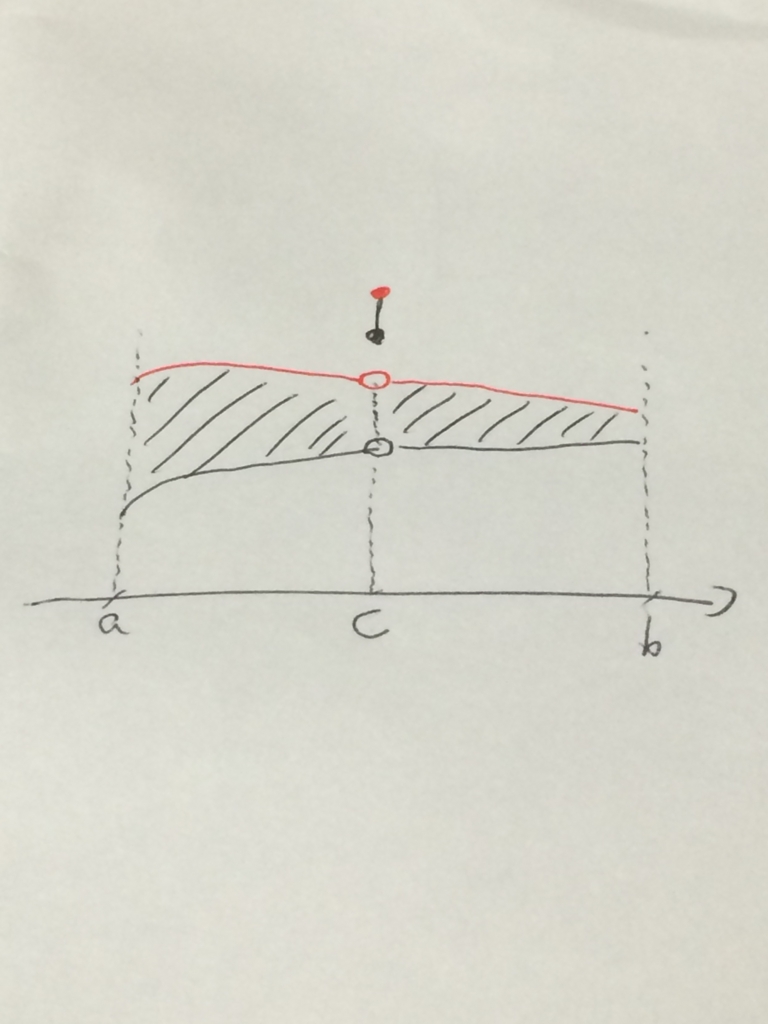
一枚目の写真と色使いは一緒である. このように, たての線( ${x=c}$ のところ)でも定義より ${U}$ の元なんだけれど, この部分では任意の近傍が ${U}$ に含まれない. したがって, これは開集合にはならない. つまり連続関数でないと開集合にならないケースがあるのだ.

これって, 少なくとも僕はこの本を読んで初めて知ったんですけど, ひょっとして常識なのかしら…….
ちなみに, ここから開円板は開集合であることが導ける. なぜなら, ${(a, b)}$ 中心の半径 ${r}$ の開円板は,
${ \begin{align} a-r < x < a+r, && b-\sqrt{r^2-(x-a)^2} < y < b+\sqrt{r^2-(x-a)^2} \end{align} }$
と不等式で定義され, ${y}$ の式の最左辺,最右辺ともに連続関数であるから, 開円板は縦線集合と結論づけられるからである.

そして, この「縦線集合は開集合である」ことの証明には, (当たり前だが) 関数の連続性を陽に使う必要がある. 実際の証明については, テキスト『微積分』を参照されたい.

まとめ

日常的に使っていると, 何がどのような命題から導出されるのかなどがよくわからなくなってくる. たとえば素因数分解の一意性はどういう命題から従うのかなど. 微積分もきっとそのひとつで, 高校時代と大学時代に二度勉強するために, 何を仮定してどのような命題を導いたのかがわかりにくくなっている.
僕はやはりきちんと微積分を勉強しなおすべきだと改めて感じた.